Research

My main research interest is spectral analysis of matrix sequences from PDE and FDE discretizations, and other structured matrices (especially Toeplitz-like), using matrix-less methods, the theory of GLT sequences, and other techniques. I especially like non-Hermitian matrix sequences with peculiar spectral behaviour. Some current projects are,

• Parallel-in-Time (PiT): Spectral analysis of associated matrices;
• Fractional derivatives (FDE): Preconditioning for iterative solvers, and spectral analysis of discretization matrices;
• Asymptotic expansion (Matrix-less methods): Eigenvalues, eigenvectors, matrix-valued and multi-variate symbols, diagonal sampling matrices, perfect grids;
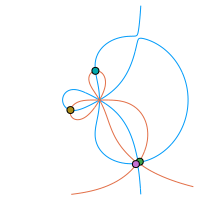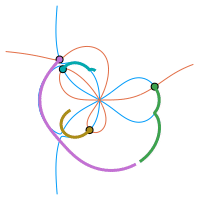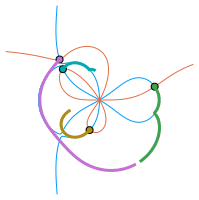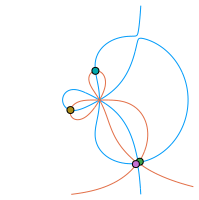
• Non-Hermitian symbols and matrix sequences: Spectral analysis of some special banded and non-banded Toeplitz and Toeplitz-like matrix sequences; e.g., \(\{T_n(f)\}_n\) for symbols \(f(z)=-z+1+z^{-1}+z^{-2}+z^{-3}\), \(z\in\mathbb{T}\), \(f(z)=\alpha z^{-r}+\beta+\gamma z^s\), \(r\neq s\in\mathbb{N}\), \(\alpha,\beta,\gamma\in\mathbb{C}\), or \(f(z)=z^{-1}(1-z)^\alpha\), \(\alpha\in(1,2)\).

My preferred research tools are Julia (with GenericLinearAlgebra.jl and GenericSchur.jl for high precision linear algebra), OEIS, RIES, Wolfram Alpha, a MacBook Air M2, an AMD Ryzen Threadripper 3970X (32 Core, 256 GB RAM), an AMD Epyc 7502P (32 Core, 1024 GB RAM, RTX 4090), clusters at UPPMAX, and an iPad Pro 12.9" with Notability.

Contact by email for questions or collaboration.